Introduction
The speculation has been for some time that computation occurs at the molecular level and is facilitated by DNA and proteins. In 1994, Leonard Adelman proved that DNA molecules in a test tube could interact to perform a complex calculation.
The central concept of this blog and current definition of “Biomatics” is the description of computational processes theoretically occurring within a single molecule. This differs from the Adelman description of DNA computation, which involves interactions of multiple molecules.
The hope is that this Blog will be of interest to Mathematicians, Biologists and Computer Scientists, as well as generally curious readers.
Naturally Occurring DNA Based Computation
Of all the scientific discoveries of the 20th century including Einstein’s Relativity, and Darwin’s Evolution none is more influential than Watson and Crick’s discovery of the structure of DNA. This is especially true in the field of computer science where every endeavor pales in comparison to the accomplishments of this incredible computing molecule.
At the single cell stage of the development of the human embryo, immediately after the sperm and egg are united, this molecule encodes the generation of an adult human being. A mere sequence of genes or base pairs would not have the computational capability to carry out this feat. The orchestrated expression of the genes in terms of a genetic alphabet would require some sort of underlying logical program carrying out some form of computation.
Leonard Adelman (1994) was the first to demonstrate how DNA can solve the Hamiltonian Path problem (similar to the Traveling Salesman problem, involving finding a path between some finite number of cities). His approach involved only the base pair sequences in a random brute force combinatorial algorithm. http://users.aol.com/ibrandt/discover_article.html This is the approach of the class of algorithms commonly known as genetic and DNA algorithms, and does not involve any digital Boolean logic. Therefore, these algorithms only begin to scratch the surface of DNA’s computational capacity.
The focus of DNA researchers has been mostly on genes while the underlying computational structure, functioning, and logic has been a mystery. Only about 5% of the genome includes the protein- coding sequences (exons) of genes. The balance of the genome is thought to consist of other noncoding regions (such as control sequences and intergenic regions), whose functioning until now are not understood, and which this blog will attempt to explore.
Computer science and Mathematics provide a wealth of tools and concepts for developing our understanding of DNA computation. Every concept of computer science can serve as a metaphor of DNA functioning. Set theory is the obvious starting point for understanding DNA. We can readily show a constructive progression from basic set theoretical concepts to Boolean algebras and algorithms. Thus, to begin, the challenge is to describe DNA in set theoretical terms. Then we can add an operation and obtain a group, or algebraic system, and then analogies with computational and mathematical concepts will flow freely. Once DNA is described as a group all the theorems of group theory become theorems of DNA.
Group theory is the study of the algebra of transformations and symmetry.
“Group Theory has emerged as a powerful tool for analyzing cognitive structure. The number of cognitive disciplines using group theory is now enormous. The power of group theory lies in its ability to identify organization, and to express organization in terms of generative actions that structure a space. ” http://www.rci.rutgers.edu/~mleyton/GT.htm
There are several ways to describe DNA as a collection of “things”:
· Genes (about 31,000 in humans)
· Base Pairs (about 3 billion)
· Atoms
· Covalent Bonds
· Conformational states
For the purposes of the present discussion, consider the ramifications of DNA as a set of conformational states.
Although DNA is usually thought of in terms of a Watson-Crick double helix, its three dimensional structure can undergo structural transitions between a number of different conformations. It seems unlikely that this phenomenon is not exploited in biological systems, especially considering the potential for information processing. The biological function of all of these DNA structures and of the transitions that occur between them cannot be understood without the input of computer scientists and mathematicians.
Conformational variation in DNA arises from restricted bond rotations, giving rise to different torsional angles at bonds connecting phosphate to ribose. Phosphate is tetrahedral like carbon, so favored conformations occur at 120 degree intervals.
http://newton.phys.keele.ac.uk/polymer/dna/dna.html
Say a DNA molecule M has N bonds capable of assuming different conformational states. For the sake of simplicity, assume two possible states per bond. Thus we have 2**N possible conformations. The total number of states is finite and can be enumerated as (S1, S2…Sn).
The Intramolecular Cube Group-
Whilst some of these changes are quite subtle, others are very dramatic and can, for example, involve a complete reversal of the handedness of the double helix. Base-pair sequence, hydration, and ionic strength in the environment of the DNA all play important parts in determining if, when, and how these transitions occur. http://newton.phys.keele.ac.uk/polymer/dna/dna.html
Consider for the sake of simplicity a chain of three carbon atoms that can each exist in one of two states. We therefore have 2**3 or eight possible states which can be labeled as 000, 001, 010, 011, 100, 101, 110, 111. To go from 000 to 001 requires the rotation of a single bond. To go from 000 to 110 requires rotation about two bonds etc. The following diagram, where the eight corners are the states and the twelve edges are the transitions between states, can depict this situation. 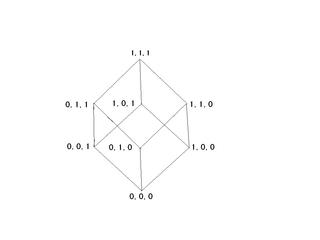
Label edges
E1 = 000,001
E2 = 001,011
E3 = 011,010
E4 = 010,000
E5 = 000,100
E6 = 100,110
E7 = 110,111
E8 = 111,011
E9 = 101,001
E10 = 111,101
E11 = 100,101
E12 = 010,110
Inverses
E1' = 001,000
E2' = 011,001
E3’ = 010,011
E4’ = 000,010
E5’ = 100,000
Etc.
If we consider all sequences of moves along the edges of the Cube, we notice the following:
Closure- One sequence followed by another sequence is a sequence.
Associativity- That is E1*(E2*E3) = (E1*E2)*E3.
Identity element- The do nothing sequence does nothing.
Inverses- Every sequence of moves can be done backwards and therefore undone, e.g. E1 and E1′.
Thus, the set of all sequences of moves on the above Cube is a group. Two sequences can be considered equivalent, in one sense, if they have the same final effect, that is they start and end at the same location. However, two different sequences can have the same beginning and end.
Coincidentally we could relabel the above cube as follows:
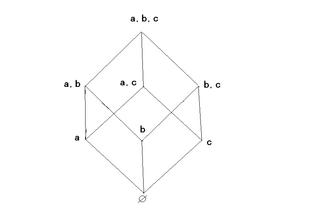
to represent the relation “containment” of one subset in another for the partially ordered set of all subsets of the set (a,b,c).
In addition, represent the relation of divisibility for the partially ordered set (1,2,3,5,6,10,15,30) as follows: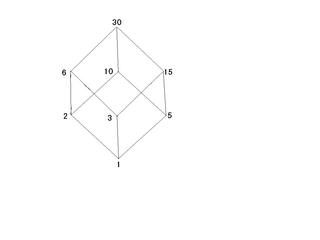
Observe that since 15 is not divisible by 10 you must move upward along an edge to get from 15 to 10.
Lagrange's theorem, the “first great result of group theory,” gives one example of the type of results that now apply:
Definition: If G is a finite group (or subgroup) then the order of G is the number of elements of G.
THEOREM: The order of a subgroup H of group G divides the order of G.
Another interesting notion is that of a Group acting on a set-
Definition: Let G be a group and let S be a set. A multiplication of elements of S by elements of G (defined by a function from G × S -> S) is called a group action of G on S provided for each x in S:
(i) a(bx) = (ab)x for all a,b in G, and
(ii) ex = x for the identity element e of G.
http://www.math.niu.edu/~beachy/aaol/frames_index.html
The challenge then is to look at the bio-chemical functioning of DNA to find where the above concepts apply in a useful manner. For example, what would be the set on which DNA acts? Several potential candidates come to mind- genetic sequences, proteins, organelles, axons, and dendrites.
We can also look to the theory of finite state machines to see what properties we can ascribe to the system. A FSM is defined by the following: a finite set of states, a finite set of inputs, and transitions mapping some state-input pairs to other states. FSM theory deals with the study of circuitry, e.g. synchronous vs. asynchronous.
To summarize, a finite state machine is described as:
An initial state
A set of possible inputs
A set of new states that may result from the input
A set of possible actions or output events that result from a new state
A Turing Machine Model offers a slightly different twist, dealing with a machines ability to read a program and deliver output:
Machine Z= (S, A, M)
1. S is a finite set of states, with distinguished element 0 (initial state)
2. A is an alphabet
3. M is a partial transition function
Intramolecular logic gates
DNA’s role as an encoder of protein production has long been understood to some degree. The conjecture here is that DNA also stores information and functionality in the conformation of its covalently bonded atoms that are able to exist in a finite number of energetically favorable states.
DNA starts out in an initial conformational state, say at the single cell stage upon conception. The transition of states thereafter defines a digital machine. Group theory and FSM theory are ways of elucidating structure in this process.
Recall the tetrahedral geometry of carbon. The rotational state of one of the four covalent bonds can be logically dependent on the other bonds in any Boolean way i.e. AND, OR, NAND, NOR.
DNA possesses an Intramolecular logical structure. An AND gate, for example, can be constructed by a single carbon atom. A shift about one of the atom’s covalent bonds can result from steric (related to the way atoms are spatially arranged) interactions caused by the conformations of the other three remaining covalent bonds (a gate with three inputs and one output). Similarly for OR gates etc. Thus, Boolean operations analogous to digital computers occur when the molecule transitions from state to state. In this way, the molecule can respond logically to external stimuli as well as orchestrate ontogenic (embryonic) development.
http://www.dnaftb.org/dnaftb/35/concept/index.html
It thus follows that DNA possesses a lattice/Boolean algebra structure, and the molecule is capable of executing digital algorithms. Not to rule out the potential for analog computation, which may also occur. At the least, we can say that one facet of DNA’s capability is discrete computation, but what level of complexity of algorithms is possible intramolecularly?
NAND gates are said to be logically complete in that any digital circuit can be constructed from them. As mentioned earlier, a carbon atom can theoretically at least act as a NAND gate. DNA however is a linear molecule and so seemingly has limited ability to join gates in a parallel fashion. The question is how DNA circumvents this apparent limitation.
The answer may lie in the interaction of the tertiary (related to folding) structure of DNA with a protein-scaffolding network.
DNA resembles a length of kite string made of legos that can fold itself into an intricate machine like network. DNA periodically coils itself around units of histones, proteins with their own incredible information processing capabilities.
Thus at the atomic level we have an intricate three-dimensional circuitry. Electrons act as switching elements, with wire the length of covalent bonds. Electronic signals are transmitted along a complex 3D switching network. Yet, there is a mechanical element to the mechanism, with groups of atoms interacting according to electromagnetic laws. One single rotation of a functional chemical group e.g. phosphate group could cause a cascade of events in a system governed by the laws of Physics, Organic Chemistry, Boolean Algebra, FSM theory, group theory, pattern recognition, etc.
http://www.dnaftb.org/dnaftb/29/concept/
Fractal geometry of DNA
Mandelbrot describes fractals as “patterns that repeat, although not necessarily in the exact same way. Through this repetition, they can provide a description of a rough, irregular surface like a coastline or a cloud.”
The repeating patterns for DNA are the processes of mitosis. Random mutations and crossovers bring about the variations, resulting in massive parallelism but with fractal differentiation. Learning is achieved through repeated minor modifications. Cells differentiate themselves gradually until at some point there is a catastrophic divergence of function, at which point one cell becomes a liver cell and the other cell becomes a brain cell for example.
Naturally Occurring Numerical Methods
Assuming then that a form of computation does occur in biological systems the question is then how similar are these processes to the principles that have been developed to date in the digital computer sciences. What data structures and algorithms does DNA utilize?
How does DNA do Math? DNA deals with analytical solutions only at a higher level of organization. At the lower levels, solutions are probably numerical, or discrete (digital). Rather than using Newton’s method to calculate an integral, DNA can approximate the answer numerically. To calculate the area under a curve DNA may approximate the answer with a finite number of data points. For example to get an estimate of the area under a curve a numerical method might be to randomly generate some data points and find what percentage fall under the curve, then multiply by the area of the rectangle containing the curve. As the number of points increases the answer approaches the analytical answer.
For more on Biomatics go to Biomatics.org:
